
Automata" redirects here. For self-operating machine, see Automaton.
In theoretical computer science, automata theory is actually the study of abstract machines and problems which they are able to solve. Automata theory is closely related to formal language theory as the automata are often classified by the class of formal languages they are able to recognize.
An automaton is a mathematical model for a finite state machine (FSM). A FSM is a machine that, given an input of symbols, "jumps", or transitions, through a series of states according to a transition function (which can be expressed as a table). In the common "Mealy" variety of FSMs, this transition function tells the automaton which state to go to next given a current state and a current symbol.
The input is read symbol by symbol, until it is consumed completely (similar to a tape with a word written on it, which is read by a reading head of the automaton; the head moves forward over the tape, reading one symbol at a time). Once the input is depleted, the automaton is said to have stopped.
Depending on the state in which the automaton stops, it's said that the automaton either accepts or rejects the input. If it landed in an accept state, then the automaton accepts the word. If, on the other hand, it lands on a reject state, the word is rejected. The set of all the words accepted by an automaton is called the language accepted by the automaton.
Note, however, that, in general, an automaton need not have a finite number of states, or even a countable number of states. Thus, for example, the quantum finite automaton has an uncountable infinity of states, as the set of all possible states is the set of all points in complex projective space. Thus, quantum finite automata, as well as finite state machines, are special cases of a more general idea, that of a topological automaton, where the set of states is a topological space, and the state transition functions are taken from the set of all possible functions on the space. Topological automata are often called M-automata, and are simply the augmentation of a semiautomaton with a set of accept states, where set intersection determines whether the initial state is accepted or rejected.
In general, an automaton need not strictly accept or reject an input; it may accept it with some probability between zero and one. Again this is illustrated by the quantum finite automaton, which only accepts input with some probability. This idea is again a special case of a more general notion, the geometric automaton or metric automaton, where the set of states is a metric space, and a language is accepted by the automaton if the distance between the initial point, and the set of accept states is sufficiently small with respect to the metric.
Automata play a major role in compiler design and parsing.
|
|
An abstract machine, also called ana abstract computer, is a theoretical model of a computer hardware or software system used in Automata theory. Abstraction of computing processes is used in both the computer science and computer engineering disciplines and usually assumes discrete time paradigm. In the theory of computation, abstract machines are often used in thought experiments regarding computability or to analyze the complexity of algorithms (see computational complexity theory). A typical abstract machine consists of a definition in terms of input, output, and the set of allowable operations used to turn the former into the latter. The best-known example is the Turing machine. More complex definitions create abstract machines with full instruction sets, registers and models of memory. One popular model more similar to real modern machines is the RAM model, which allows random access to indexed memory locations. As the performance difference between different levels of cache memory grows, cache-sensitive models such as the external-memory model and cache-oblivious model are growing in importance. An abstract machine can also refer to a microprocessor design which has yet to be (or is not intended to be) implemented as hardware. An abstract machine implemented as a software simulation, or for which an interpreter exists, is called a virtual machine. Through the use of abstract machines it is possible to compute the amount of resources (time, memory, etc.) necessary to perform a particular operation without having to construct an actual system to do it.  | state automaton (plural: automata) or simply a state machine, is a model of behavior composed of a finite number of states, transitions between those states, and actions. A finite state machine is an abstract model of a machine with a primitive internal memory.
A current state is determined by past states of the system. As such, it can be said to record information about the past, i.e., it reflects the input changes from the system start to the present moment. A transition indicates a state change and is described by a condition that would need to be fulfilled to enable the transition. An action is a description of an activity that is to be performed at a given moment. There are several action types:
An FSM can be represented using a state diagram (or state transition diagram) as in figure 1 above. Besides this, several state transition table types are used. The most common representation is shown below: the combination of current state (B) and condition (Y) shows the next state (C). The complete actions information can be added only using footnotes. An FSM definition including the full actions information is possible using state tables (see also VFSM). 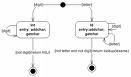 |